Question

Express the vector in component form given its magnitude is 12 and direction angle is 220 degrees

Answer 1

The components of a vector of magnitud A and direction θ can be written as follow:

`\begin{gathered} A_x=Acosθ \\ A_y=Asin\theta \end{gathered}`

where Ax is the x-component of A vector and Ay is the y-component.

In this case, you have that magnitude of A is A = 12 and direction θ is θ = 220°, then, by replacing these values into the expressions for Ax and Ay, you get:

`\begin{gathered} A_x=12cos220°=-9.19 \\ A_y=12sin220°=-7.71 \end{gathered}`

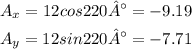
Hence, the components of the given vector are <-9.19 , -7.71>