Question

There is a game where the outcome is a random integer from 1 to 20, costing $15 to enter. If the outcome is even, you win $28. If the outcome is odd, you win nothing. If you play the game, what is the expected profit?

Answer 1

In the game, the outcome is a random integer from 1 to 20.

-If the outcome is even, you win $28

-If the outcome is odd, you win nothing ($0)

There are 10 even numbers and 10 odd numbers between 1 and 20.

The probability of choosing one even number at random can be calculated as the quotient between the number of even numbers and the total number of numbers:

`P(even)=(10)/(20)=(1)/(2)`

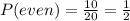
The probability of choosing an odd number at random can be calculated using the same logic, it is the quotient between the number of even numbers and the total number of numbers:

`P(odd)=(10)/(20)=(1)/(2)`

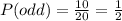
Let "X" represent the winnings after choosing a number at random, there are two possible outcomes, to win $28 or to win nothing ($0), you can arrange the data on a probability table:

The expected value is equal to the sum of the product between each possible observation and it