Question

Need help with this review question how would I know if they are congruent?

Answer 1

Step-by-step explanation

A chord is a line segment joining two points on a circumference. If two different chords share one of their extremes then they form an angle known as an inscribed angle. The other extremes of these chords form an arc that is known as the intercepted arc of the inscribed angle. For example, in the picture you'll notice that chords AD and DB form the angle ADB and its intercepted arc is arcAB. The measure of an inscribed angle is half the aperture of its intercepted arc so we get:

`\angle ADB=(1)/(2)\measuredangle arcAB`

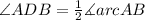
Angle ACB also has arcAB as its intercepted arc. This means that we also have:

`\begin{gathered} \angle ACB=(1)/(2)\measuredangle arcAB=\angle ADB \\ \angle ACB=\angle ADB \end{gathered}`

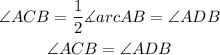
So angles ACB and ADB are congruent since they have the same measure. So as you can see, if two inscribed angles have the same intercepted arc they are congruent.

Angles CAD and CBD also share the same intercepted arc, arcCD. This means that this angles are also congruent.

ADB and CAD are not congruent because their intercepted arcs (arcAB and arcDC) are not the same. The same happens with BCA and CBA since their intercepted arcs are arcAB and arcBC.

The last pair of angles that we must analyze is the one composed by DEA and CEB. These two angles are formed at the intersection between two line segments. At this type of intersections four angles are formed with consecutive angles being supplementary and opposite angles being congruent. DEA and CEB are opposite angles since they share their vertex but not their sides. Therefore DEA and CEB are congruent.

Answer

Then the correct options are A, C and D.