Question

Suppose that shoe sizes of American woman have a bell shaped distribution with a mean of 8.04 And a standard deviation of 1.53 using the empirical rule what percentage of American woman have shoe sizes that are less than 11 point one please do not round your answer

Answer 1

Step 1

Given; Suppose that shoe sizes of American women have a bell-shaped distribution with a mean of 8.04 And a standard deviation of 1.53.

Required; using the empirical rule what percentage of American women have shoe sizes that are less than 11.1. please do not round your answer.

Step 2

The empirical rule states that for a normal distribution, 68% of the distribution are within one standard deviation from the mean, 95% are within two standard deviations from the mean and 99.7% are within three standard deviations from the mean.

Given that:

`\begin{gathered} mean(\mu)=8.04 \\ Standard\text{ deviation\lparen}\sigma)=1.53 \\ \end{gathered}`

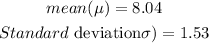
68% are within one standard deviation

`\mu\pm\sigma=8.04\pm1.53=(6.51,9.57)`

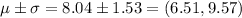
95% are within two standard deviation

`\mu\pm2\sigma=8.04\pm2(1.53)=(4.98,11.1)`

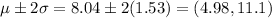
Thus, we can see that the American women have shoe sizes that are no more than 11.1 will be;

`95\text{\%+\lparen}(100-95)/(2))\text{\%=95+2.5=97.5\%}`

Answer;

`The\text{ American women with a shoe size that are less than 11.1=97.5\%}`