Given the table:
Time(years) 0 1 2 3
Value(dollars) 20,000 18,000 16,200 14,580
Let's determine the correct statement.
Here, we can see that as the time increases, the value decreases.
So, the situation can be modelled using a decay function.
Now, let's find the decay rate.
Apply the formula:
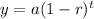
Where:
a is the initial value.
y is the value in dollars at t, time.
r is the decay rate.
We have:
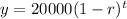
Now use any of the values to solve for r.
Plug in 18000 for y and 1 for t.
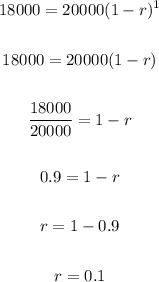
The decay rate is 0.1
Let's convert the rate to percent.
Percent change = 0.1 x 100 = 10%
Therefore, the situation can be modeled by an exponential decay function with a percent change of -10%.
ANSWER:
D. The situation can be modeled by an exponential decay function with a percent change of -10%.