Question

Calculate final velocities assuming elastic collisions.m1=20 kg V01= 4 m/s m2=10 kg Vo2= 0 m/sVf1m/s (Round to 2 significant figures)V=2=m/s (Round to 2 significant figures)

Answer 1

Since the collision is elastic, the total kinetic energy of the system will remain the same after the collision.

For the conservation of momentum, we have the following equation:

`\begin{gathered} m_1v_(o1)+m_2v_(o2)=m_1v_(f1)+m_2v_(f2) \\ 20\cdot4+10\cdot0=20\cdot v_(f1)+10\cdot v_(f2) \\ 20v_(f1)+10v_(f2)=80 \\ 2v_(f1)+v_(f2)=8 \end{gathered}`

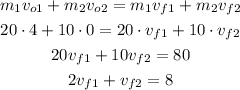
Now, from the kinetic energy conservation, we have:

`\begin{gathered} (m_1v^2_(o1))/(2)+\frac{m^{}_2v^2_(o2)}{2}=(m_1v^2_(f1))/(2)+(m_2v^2_(f2))/(2) \\ m_1v^2_(o1)+m_2v^2_(o2)=m_1v^2_(f1)+m_2v^2_(f2) \\ 20\cdot4^2+10\cdot0=20\cdot v^2_(f1)+10\cdot v^2_(f2) \\ 20v^2_(f1)+10v^2_(f2)=320 \\ 2v^2_(f1)+v^2_(f2)=32 \end{gathered}`

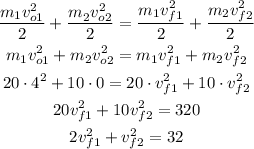
From the first equation, we have vf2 = 8 - 2vf1. Using this value on the second equation, we have:

`\begin{gathered} 2v^2_(f1)+(8-2v^{}_(f1))^2=32 \\ 2v^2_(f1)+64-32v^{}_(f1)+4v^2_(f1)=32 \\ 6v^2_(f1)-32v^{}_(f1)+32=0 \end{gathered}`

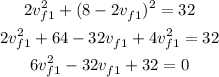
Solving this quadratic equation, we have vf1 = 1.33 or vf1 = 4.

vf1 = 4 represents the initial situation, before the collision, so we have vf1 = 1.33 m/s.

Calculating vf2, we have:

`\begin{gathered} v_(f2)=8-2\cdot1.33 \\ v_(f2)=8-2.66 \\ v_(f2)=5.33 \end{gathered}`

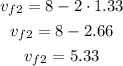
Rounding to two significant figures, we have vf1 = 1.3 m/s and vf2 = 5.3 m/s.