We are given that the height of an object that is moving in projectile motion is the following:
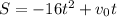
Where:
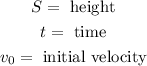
Now we will substitute the value of S for 272 ft, we get:
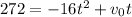
Now we subtract 272 from both sides, we get:
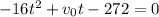
We get an equation of the form:
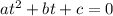
The value of "t" are determined using the quadratic formula:
![t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/3cgw61gskglny4a505tle5b9wokluktv58.png)
Substituting the values we get:
![t=\frac{-v_0\pm\sqrt[]{v^2_0-4(-16)(-272)}}{2(-16)}](https://img.qammunity.org/2023/formulas/physics/college/xgpoqm33m6lc81dl9rmz59ubg170fiutr4.png)
Solving the operations we get:
![t=\frac{-v_0\pm\sqrt[]{v^2_0-17408}}{-32}](https://img.qammunity.org/2023/formulas/physics/college/xo8kdxg8nm0xidi9kisedjpmaga3lqhpgp.png)
Therefore, we get two possible values for the time:
![t_1=\frac{-v_0+\sqrt[]{v^2_0-17408}}{-32}](https://img.qammunity.org/2023/formulas/physics/college/dfai0gm0iyoqh93w8xe0x6w0yk2s3jtk9g.png)
The second value is:
![t_2=\frac{-v_0-\sqrt[]{v^2_0-17408}}{-32}](https://img.qammunity.org/2023/formulas/physics/college/i9byjdug13l5izzkacpmknikon3prnghow.png)
Part b. We are asked to determine the time when the object returns to the ground and the initial velocity is 32 ft/s. To do that we will use the formula for the height:
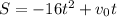
Now we substitute the value of the initial speed:
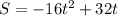
Now, since we want the time when the object returns to the ground this means that the height must be zero, therefore, we substitute the values S = 0, we get:
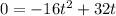
Now we take "t" as a common factor:
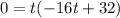
Now we set each factor to zero:
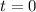
For the second factor we get:
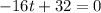
Now we subtract 32 from both sides:
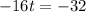
Now we divide both sides by -16:
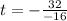
Solving the operations:
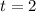
Therefore, in 2 seconds the object will return to the ground.