Question

Determine the center and radius of the circle described by the equation

Answer 1

Step 1:

To find the equation of a circle when you know the radius and center, use the formula.

`(x\text{ - a\rparen}^2\text{ + \lparen y - b\rparen}^2\text{ = r}^2`

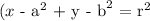
Where (a, b) represents the center of the circle, and r is the radius. This equation is the same as the general equation of a circle, it's just written in a different form.

Step 2

`\begin{gathered} (x\text{ + 1\rparen}^2\text{ + \lparen y - 3\rparen}^2\text{ = 9} \\ \\ (x\text{ + 1\rparen}^2\text{ + \lparen y - 3\rparen}^2\text{ = 3}^2 \\ \\ a\text{ = -1, b = 3, r = 3} \\ \\ Center\text{ = \lparen-1, 3\rparen and radius r = 3} \end{gathered}`

Final answer

Center = (-1 , 3)

Radius r = 3