Question

The area of an equilateral triangle is 36√3 cm^2. What is the height of the triangle?A. 6 cmB. 12 cmC. 6√3 cmD. 12√3 cm

Answer 1

The area of a triangle is given by the expression:

`A_{\text{triangle}}=(1)/(2)b\cdot h`

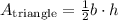
Where b is the basis and h is the height.

Then, in the case of our problem:

`(1)/(2)b\cdot h=36\sqrt[]{3}`

There is something particular of the equilateral triangles, see the diagram below:

Notice that we can use trigonometric identities to find an expression that involves the length of a side and the height.

We can use the sine function

`\begin{gathered} \sin (\theta)=(O)/(H) \\ \Rightarrow\sin (60degree)=(h)/(b) \end{gathered}`

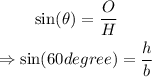
Furthermore, the exact value of sin(60°) is sqrt(3)/2

`\sin (60degree)=\frac{\sqrt[]{3}}{2}`

Therefore:

`\begin{gathered} \frac{\sqrt[]{3}}{2}=(h)/(b) \\ \Rightarrow b=\frac{h}{\frac{\sqrt[]{3}}{2}}=\frac{2h}{\sqrt[]{3}} \end{gathered}`

Finally, we can substitute this last result in the equation for the area of the triangle:

`\begin{gathered} (1)/(2)b\cdot h=36\sqrt[]{3} \\ \Rightarrow(1)/(2)(\frac{2h}{\sqrt[]{3}})\cdot h=36\sqrt[]{3} \\ \Rightarrow h^2=\frac{2\cdot\sqrt[]{3}}{2}(36\sqrt[]{3}) \end{gathered}`

We only need to simplify and solve for h, as shown below:

`\begin{gathered} \Rightarrow h^2=36\cdot3 \\ \Rightarrow h=\sqrt[]{36\cdot3}=6\sqrt[]{3} \end{gathered}`

The solution is then h=6*sqrt(3), option C

Explanation for sin(60°)=sqrt(3)/2

Actually, we can use an equilateral triangle which basis is equal to 1 to prove this:

The blue line is the height, and notice that it crosses the basis in the middle, so the orange segment is equal to 1/2. We can then use the Pythagoras Theorem to find the value of the blue segment:

`\begin{gathered} x^2+((1)/(2))^2=1^2=1 \\ \Rightarrow x=\sqrt[]{1-(1)/(4)}=\sqrt[]{(3)/(4)}=\frac{\sqrt[]{3}}{2} \end{gathered}`

Furthermore, we know that the identity sin(theta)=O/H, then:

`\sin (60degree)=(O)/(H)=\frac{\frac{\sqrt[]{3}}{2}}{1}=\frac{\sqrt[]{3}}{2}`