Question

A ball is thrown from an initial height of 2 feet with an initial upward velocity of 30 ft/s. The ball’s height h (in feet) after t seconds is given by the following.h=2+30t-16t^2 Find all values of t for which the ball’s height is 10 feet. Round your answer to the nearest hundredth.

Answer 1

To determine the value of t in a given function:

`h=2+30t-16t^2`

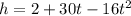
The ball’s height h (in feet) after t seconds is given by the following.

`\begin{gathered} h=2+30t-16t^2 \\ \text{where h = height =10 f}eet \\ 10=2+30t-16t^2 \end{gathered}`

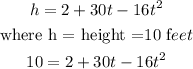
Collect like terms and Solve using formular method

`\begin{gathered} 16t^2-30t+8=0 \\ \frac{-b\pm\sqrt[]{b^2}-4ac}{2a} \\ a=16\text{ , b = -30 , c = 8} \end{gathered}`
`\begin{gathered} t=\frac{-b\pm\sqrt[]{b^2}-4ac}{2a}=\frac{--30\pm\sqrt[]{(-30)^2-4(16)(8)}}{2(16)} \\ t=\frac{30\pm\sqrt[]{900-512}}{32}=\frac{30\pm\sqrt[]{388}}{32}=(30\pm19.69)/(32) \\ t=(30+19.69)/(32)\text{ OR }(30-19.69)/(32) \\ t=\text{ 1.553 or 0.322} \\ t=1.55\text{ or 0.32 (nearest hundredth)} \end{gathered}`

Therefore the values of t for ball’s height is 10 feet are t = 1.55 or 0.32 (nearest hundredth)