Given:
The length of the greenhouse is 6m.
The sectoral angle of ABD is 120 degrees.
The radius of the sector is r=2m.
The length of the line segment BC is b=1m
To find the volume of the greenhouse:
The formula of the volume of the greenhouse is given below,
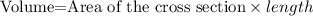
Let us first find the area of the cross-section.
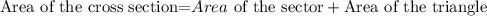
Using the formula of area of the sector and area of the triangle,
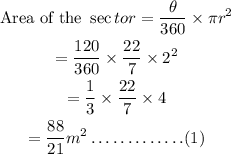
From the triangle BCD, using Pythagoras theorem to find the height CD,
![\begin{gathered} BD^2=BC^2+CD^2 \\ 2^2=1^2+CD^2 \\ 4-1=CD^2 \\ CD^2=3 \\ CD=\sqrt[]{3}m \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/v6j7130dzzdzuh1je95sctvzev5nhse69r.png)
So, the area of the triangle is,
![\begin{gathered} A=(1)/(2)* b* h \\ =(1)/(2)*1*\sqrt[]{3} \\ =\frac{\sqrt[]{3}}{2}m^2\ldots\ldots\ldots\ldots\text{.}(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zqe9lvml7rhl6yxfz3s19r8js5smcp75yt.png)
Adding (1) and (2) we get,
![\begin{gathered} \text{Area of the cross section =}(88)/(21)+\frac{\sqrt[]{3}}{2} \\ =\frac{176+21\sqrt[]{3}}{42}m^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8xr3qcf1pavnm4ay39gnja33k9hkhlvc23.png)
Using this value in the volume formula we get,
![\begin{gathered} V=\frac{(176+21\sqrt[]{3})}{42}*6 \\ =\frac{176+21\sqrt[]{3}}{7}m^3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3zdvcbhpzq86enyv4u54s3vzjs95i0ewug.png)
Hence, the volume of green house is,
![\begin{gathered} \frac{176+21\sqrt[]{3}}{7}m^3 \\ (or) \\ 30.34m^3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/g1xucxpoo4wbcmoai3ja07pnxbqjy602np.png)