Question

Feb 26, 8:23:30 PM A manufacturer of ski clothing makes ski pants and ski jackets. The profit on a pair of ski pants is $3 and on a jacket is $7. Both pants and jackets require the work of sewing operators and cutters. There are 60 minutes of sewing operator time and 48 minutes of cutter time available. It takes 8 minutes to sew one pair of ski pants and 4 minutes to sew one jacket. Cutters take 4 minutes on pants and 8 minutes on a jacket. The manufacturer wants to make a minimum of 4 ski pants and 2 ski jackets. Let x represent the number of ski pants. Let y represent the number of ski jackets, y > 2 8x - 4y < 96 43 - 8772 Find the maximum profit and the amount of pants and jackets to maximize the profit.

Answer 1

∵ Since they will make 4 pants and 2 jackets

∵ The profit of a pair of pants is $3

∵ The profit of a jacket is $7

∴ P = 3x + 7y

We will take the vertices of the shaded area and substitute them in the equation above to find the maximum profit.

∵ The vertices are (4, 7), (4, 2), (11, 2), (10, 4)

∵ x = 4 and y = 7

`\begin{gathered} \therefore P=3(4)+7(7) \\ \therefore P=12+49 \\ \therefore P=61 \end{gathered}`

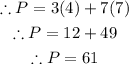
∵ x = 4 and y = 2

`\begin{gathered} \therefore P=3(4)+7(2) \\ \therefore P=12+14 \\ \therefore P=26 \end{gathered}`

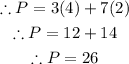
∵ x = 11 and y = 2

`\begin{gathered} \therefore P=3(11)+7(2) \\ \therefore P=33+14 \\ \therefore P=47 \end{gathered}`

∵ x = 10 and y = 4

`\begin{gathered} \therefore P=3(10)+7(4) \\ \therefore P=30+28 \\ \therefore P=58 \end{gathered}`

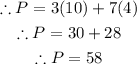
The maximum value is $61

∴ The maximum profit is $61

∴ The amounts for the maximum profit are 4 pair of pants and 7 jackets