Solution
Step 1:
Write the mid-point formula
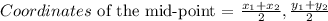
Step 2:
W is a midpoint of OR
Coordinate of 0 = (0,0) and thw coordinate of R = (4a,4b)

Step 3:
Z is the mid-point of TS
Coordinates of T = (4e, 0) and the coordinates of S = (4c, 4d)
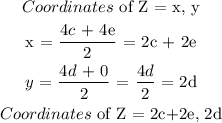
Final answer
c. W (2a , 2b) , Z (2c + 2e, 2d)