Question

Solve the inequality and represent the solution in the number line:5x - (x + 2) > -5(1 + x) +3

Answer 1

`5x-(x+2)>-5(1+x)+3`

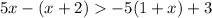
We can begin by eliminating the parentheses by distributing the terms:

`5x-x-2>-5-5x+3`

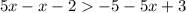
Reducing like terms at either side of the equation:

`4x-2>-2-5x`

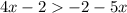
Adding 2 at both sides:

`\begin{gathered} 4x-2+2>-2+2-5x \\ \\ 4x>-5x \end{gathered}`

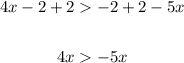
Now adding 5x at both sides:

`\begin{gathered} 4x+5x>-5x+5x \\ \\ 9x>0 \\ \\ x>0 \end{gathered}`

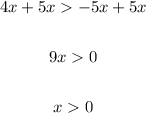
Then, the solution for the inequality is the set of all real numbers higher than 0 (excluding it).

We can represent this in the number line by highlighting all positive numbers and drawing a void circle at 0 to indicate that the solution does not include it: