Answer:
HCF =

Explanation:
A common factor is a factor that is shared by two or more numbers (or, in this case, polynomials). The highest common factor (HCF) is found by finding all common factors of the two expressions and selecting the largest one.
Find HCF of
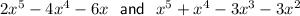
Factor
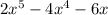
Factor out common term:
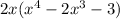
Factor
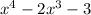 :
:

Factor
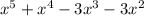
Factor out common term:
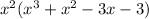
Factor
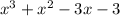 :
:
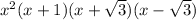
Therefore, from inspection the HCF =
