Question

Mrs. Stark has 78 Algebra II students who took the Statistics Assessment. The scoresare normally distributed, with a mean of 82.3 and a standard deviation of 3.5.Approximately, how many students scored between an 80 and a 90 on thisassessment?

Answer 1

To check how many students scored between this range, we need to calculate the area of the distribution inside this range. To do that, we're going to use a z-table.

A z-table is a table with the correspondence between the z-score and the area below the graph. To use a z-table, first we need to convert those student scores to z-scores, and we do that using the following formula:

`z=(x-\mu)/(\sigma)`

From the question text, we have the following information:

`\begin{gathered} \mu=82.3 \\ \sigma=3.5 \\ x_1=80 \\ x_2=90 \end{gathered}`

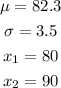
Turning this into z-scores, we have:

`\begin{gathered} z_1=((80-82.3))/(3.5)\approx-0.66 \\ z_2=((90-82.3))/(3.5)=2.2 \end{gathered}`

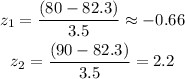
For each z-score, we have the following area:

`\begin{gathered} A_1=0.2454 \\ A_2=0.4861 \end{gathered}`

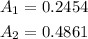
If you sum them up, you're going to get the percentage of students between this range:

`A_1+A_2=0.7315`

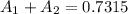
Now, we know 73.15% of the students had a score between 80 and 90. Since the total amount of students is 78 we just calculate the percentage out of this value:

`(73.15)/(100)*78\approx57`

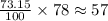
Then, we have our answer.

Approximately 57 students scored between an 80 and a 90