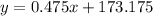Question

Find the equation of the line that passes through (27,186) and (67,205) in slope intercept form

Answer 1

The equation of a line passing through points (x₁, y₁) and (x₂, y₂) is given by:

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)`

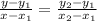
In this problem, we have:

x₁ = 27

y₁ = 186

x₂ = 67

y₂ = 205

So, we can use those values in the above formula to find the equation of the line:

`\begin{gathered} (y-186)/(x-27)=(205-186)/(67-27) \\ \\ (y-186)/(x-27)=(19)/(40) \end{gathered}`

Now, we can multiply both sides of the equation by the factor (x - 27):

`\begin{gathered} (y-186)/(x-27)(x-27)=(19)/(40)(x-27) \\ \\ y-186=(19)/(40)x-(513)/(40) \end{gathered}`

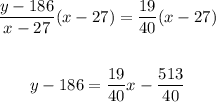
Finally, the equation in slope-intercept form requires y to be isolated on one side of the equation. So, we need to add 186 to both sides to put the equation in this form:

`\begin{gathered} y-186+186=(19)/(40)x-(513)/(40)+186 \\ \\ y=(19)/(40)x+(-513+186\cdot40)/(40) \\ \\ y=(19)/(40)x+(7440-513)/(40) \\ \\ y=(19)/(40)x+(6927)/(40) \\ \\ y=0.475x+173.175 \end{gathered}`

Notice you can write the slope and the intercept of the equation using fractions or decimal form.

The slope is the number multiplying x (0.475), while the y-intercept is the constant 173.175.

Therefore, the equation of the line that passes through (27,186) and (67,205) in slope-intercept form is

`y=0.475x+173.175`