Question

Using synthetic division, determine whether the numbers are zeros of the polynomial function.

Answer 1

Given:

`f(x)=3x^3+7x^2-14x+24`

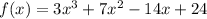
Let's use synthetic division to find the zeros.

Given: x = -4, 3

Let's first find f(-4) and f(-3).

Substitute -4 for x and solve for f(-4):

`\begin{gathered} f(-4)=3(-4)^3+7(-4)^2-14(-4)+24 \\ \\ f(-4)=-192+112+56+24 \\ \\ f(-4)=0 \end{gathered}`

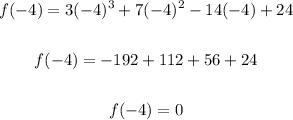
Since f(-4) = 0, it means that -4 is a zero of the function.

Also let's solve for f(-3):

`\begin{gathered} f(3)=3(3)^3+7(3)^2-14(3)+24 \\ \\ f(3)=81+63-42+24 \\ \\ f(3)=126 \end{gathered}`

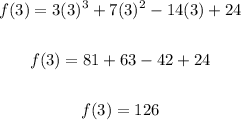
-3 is not a zero.

Now, let's perform a synthetic division using the known zero: x = -4.

To divide, set the numbers representing the dividend and the divisor in the long division like method then perform the division.

We have:

The numbers below the division line represents the quotient except the last number which is the remainder.

Thus, we have:

`f(x)=(x+4)(3x^2-5x+6)`

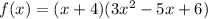
The expression cannot be factored any further.

Since it cannot be factored any further, we have only one zero which is:

x = -4.

Therefore, the number -4 is a zero of the polynomial function because f(-4) = 0 and the number 3 is not a zero of the function because f(3) = 126.

• ANSWER:

A. The number -4 is a zero of the polynomial function because f(-4) = 0 and the number 3 is not a zero of the function because f(3) = 126.