Given:
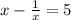
Asked: Find the value of:
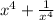
Solution:
First, we need to find the value of x through the given.
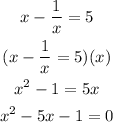
We arrived with a quadratic equation so we will use this formula:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{when }ax^2+bx+c=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6l29vqco31j4fdz65ymu4cqtbdu5eraqi0.png)
Now, let's substitute the equation we have to the formula where a = 1, b = -5 and c = -1.
![undefined]()