To solve these diamond problems you have to follow the given diagram. The values are on the left (x) and right (y) cells, to determine the value that corresponds to the top cell, you have to multiply both values.
To determine the value that corresponds to the bottom cell, you have to add both values.
On the second diamond problem, you have to work backward. The values of x and y are unknown, but we know the result of their multiplication and their addition:
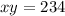
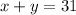
To determine the values of x and y you have to work as if it is a system of equations, first write the second expression in terms of one of the variables, for example, write it for y:
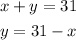
Next, replace the expression obtained for y on the first equation and solve for x:
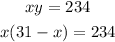
-Distribute the multiplication on the parentheses term:
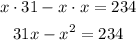
-Pass 234 to the left side of the equation to zero the equation and order the terms from greatest to least:
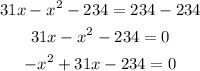
To determine the value of x you can use the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where
a is the coefficient of the quadratic term
b is the coefficient of the x-term
c is the constant
For our quadratic equation, the coefficients are: a=-1, b=31, and c=-234
Replace these values on the formula and solve:
![\begin{gathered} x=\frac{-31\pm\sqrt[]{(31)^2-4\cdot(-1)(-234)}}{2\cdot(-1)} \\ x=\frac{-31\pm\sqrt[]{961-936}}{-2} \\ x=\frac{-31\pm\sqrt[]{25}}{-2} \\ x=(-31\pm5)/(-2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tip3cz2y9hp66zkbb53zv83bodixe9ukfh.png)
Now, you have to solve the addition and subtraction separately:
Addition:
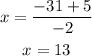
Subtraction:
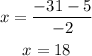
Choose either one value of x, to determine the corresponding value of y:
For x=13
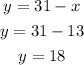
So the result of the diamond problem is: