Question

A crate is at rest on an inclined plane. As the slope increases the crate remains at rest until the incline reaches an angle of 32.7° from the horizontal. At this angle the crate begins to slidedown the ramp.What is the coefficient of static friction between the crate and the surface of the ramp?

Answer 1

The free body diagram of the crate can be shown as,

According to free body diagram, the net force acting on the crate is given as,

`F=mg\sin \theta-f\ldots\ldots\text{ (1)}`

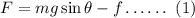
The frictional force acting on the crate is,

`f=\mu N`

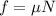
According to free body diagram, the normal force acting on the crate is,

`N=mg\cos \theta`

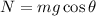
Therefore, the frictional force becomes,

`f=\mu mg\cos \theta`

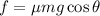
Since, the crate is at rest therefore, according to Newton's second law of motion, the net force acting on the crate is,

`F=0`

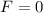
Substitute the known values in the equation (1),

`\begin{gathered} 0=mg\sin \theta-\mu mg\cos \theta \\ mg\sin \theta=\mu mg\cos \theta \\ \mu=(\sin \theta)/(\cos \theta) \\ =\tan \theta \end{gathered}`

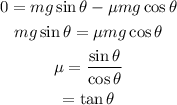
Plug in the known values,

`\begin{gathered} \mu=\tan 32.7^(\circ) \\ \approx0.642 \end{gathered}`

Thus, the coefficient of static friction between the crate and surface of ramp is 0.642.