Step-by-step explanation:
13) The number of cycles of the periodic wave per unit time is called the wave's frequency.
14)
Given:
A pendulum makes 40 vibrations in 20 seconds.
To find:
The period of the pendulum
Step-by-step explanation:
The period of the pendulum is the time taken by the pendulum to perform one vibration/oscillation/cycle. Thus,

Final answer:
Thus, the period of the pendulum is 0.5 seconds.
15) The frequency is the reciprocal of the time period meaning it is inversely proportional to the time period. Thus, as the frequency of the wave increases, the time period of the wave decreases.
16) The wavelength and frequency of a wave are related as:
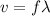
Rearranging above equation, we get:
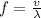
We see that the frequency and the wavelength are inversely proportional to each other. In a uniform medium, the speed of the wave will remain constant. Thus, as the wavelength of the wave increases, its frequency decreases.
17)
Given:
Frequency of wave: f = 20 Hz
The wavelength of wave: λ = 0.50 m
To find:
The speed of the wave.
The wavelength and frequency of a wave are related as:
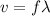
Here, v is the velocity of the wave.
Substitute the values in the above equation and simplify, we get:
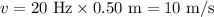
Final answer:
Thus, the speed of the wave is 10 m/s.
18)
Given:
The period of the wave is: T = 0.0300 s
The velocity of wave is: v = 10.0 m/s
To find:
The frequency and the wavelength of the wave.
Step-by-step explanation:
The frequency is the reciprocal of the time period. Thus,
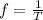
Here, f is the frequency and T is the time period.
Substitute the values in the above equation and simplify, we get:
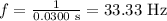
The frequency, the wavelength, and the speed are related as:
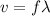
Rearranging above equation, we get:
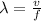
Substitute the values in the above equation and simplify, we get:
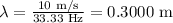
Final answer:
Thus, the frequency of a wave is 33.33 Hz and the wavelength of the wave is 0.3000 m.
19)
Given:
The wavelength of a wave is: λ = 4 m.
Speed of the wave is: v = 3 m/s
To find:
The frequency and the period of the wave.
Step-by-step explanation:
The frequency, the wavelength, and the speed are related as:
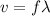
Rearranging above equation, we get:
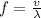
Substitute the values in the above equation and simplify, we get:
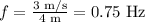
Frequency is the reciprocal of the time period, thus
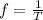
Rearranging the above equation, we get:
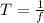
Substitute the value of frequency and simplify as:
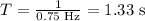
Final answer:
Thus, the frequency of wave is 0.75 Hz and the time period of wave is 1.33 s.