Given:
The acceleration of the child, a=1.26 m/s²
The angle of inclination, θ=28°
To find:
The coefficient of kinetic friction between the child and the slide.
Step-by-step explanation:
The net force acting on the child when it is sliding down the slide is given by,
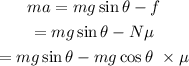
Where f is the frictional force, N is the normal force acting on the child, g is the acceleration due to gravity, and μ is the coefficient of kinetic friction.
On simplifying the above equation,
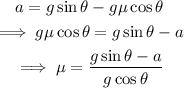
On substituting the known values,
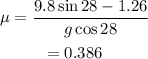
Final answer:
The coefficient of kinetic friction between the child and the slide is 0.386