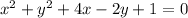The given center is (-2,1), which means h = -2 and k = 1. We also know that the circle passes through (-4,1), which means x = -4 and y = 1.
Let's use the standard form first

Let's replace the given information to find r
![\begin{gathered} (-4-(-2))^2+(1-1)^2=r^2 \\ r=\sqrt[]{(-4+2)^2}=\sqrt[]{(-2)^2} \\ r=\sqrt[]{4}=\pm2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hptmhqyd3srfc7ggfwppoekj6wdzca3xup.png)
Once we have r, we can look for the general form
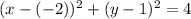
Then, we solve the binomials
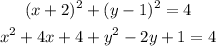
At last, we organize all the terms and the left side.
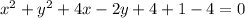
Hence, the general form is