ANSWER
2
Step-by-step explanation
We are given the function:
f(x) = 2x - 5
We want to construct the difference quotient:
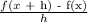
To find f(x + h), we replace x in the function with (x + h):
f(x + h) = 2(x + h) - 5
f(x + h) = 2x + 2h - 5
Therefore, the difference quotient is:

That is the simplified difference quotient.