Question

For the function f(x) = 2x - 5, construct and simplify the difference quotient [f(x + h) - f(x)] / h

Answer 1

2

Step-by-step explanation

We are given the function:

f(x) = 2x - 5

We want to construct the difference quotient:

`\frac{f(x\text{ + h) - f(x)}}{h}`

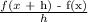
To find f(x + h), we replace x in the function with (x + h):

f(x + h) = 2(x + h) - 5

f(x + h) = 2x + 2h - 5

Therefore, the difference quotient is:

`\begin{gathered} \frac{2x\text{ + 2h - 5 - (2x - 5)}}{h} \\ \frac{2x\text{ + 2h - 5 - 2x + 5}}{h} \\ (2h)/(h) \\ \Rightarrow\text{ 2} \end{gathered}`

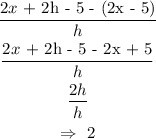
That is the simplified difference quotient.