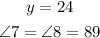Given:
Line C intersects line D in the given figure.
Required:
(a) Classify the relation between angle 7 and angle 8.
(b) Explain the angles created by the intersection of lines C and D to solve for y.
(c) Solve for y and find the measure of angles 7 and 8.
Step-by-step explanation:
(a) The lines C and D intersect each other so the angles 7 and 8 will be equal by the property of vertically opposite angles.
(b) Since vertically opposite angles are equal so angles 5y-29 and 3y+19 will be equal.
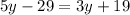
By solving the above equation we can find the value of y.
(c)
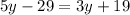
Subtract 3y on both sides.
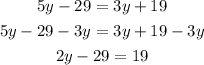
Add 29 on both sides.
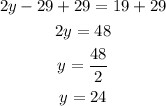
We know that the sum of linear angles is 180 degrees.
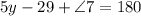
Substitute the value of y.
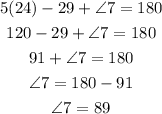
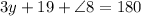
Substitute the value of y.
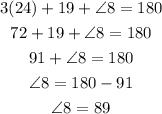
Final Answer:
(a) Angle 7 and angle 8 are vertically opposite angles.
(b)
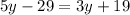
(c)