Question

Select the correct answer from each drop-down menu. The function relates the age of a plant fossil, in years, to the percentage, of carbon-14 remaining in the fossil relative to when it was alive. t(c) = -3,970.9(Inc) Use function to complete the statements. A fossil with 47% of its carbon-14 remaining is approximately A fossil that is 7,000 years old will have approximately years old. of its carbon-14 remaining.

Answer 1

Step-by-step explanation:

The equation t(c) = -3,970.9 (ln c) relates the age of a plant fossil t and the percentage of carbon-14 c.

So, To know the age of a plant fossil with 47% of its carbon-14 remaining, we need to replace c by 0.47 and calculated t(c) as:

`\begin{gathered} t(c)=-3970.9(\ln \text{ c)} \\ t(c)=-3970.9(\ln \text{ 0.47)} \\ t\mleft(c\mright)=2998.11 \end{gathered}`

Therefore, A fossil with 47% of its carbon-14 remaining is approximately 2998 years old.

On the other hand, to know the percentage of carbon remaining in a fossil that is 7,000 years old, we need to replace t(c) by 7,000 and calculate the value of c. Then:

`\begin{gathered} t(c)=-3970.9(\ln \text{ c)} \\ 7000=-3970.9(\ln \text{ c)} \\ (7000)/(-3970.9)=\ln \text{ c} \\ -1.76=\ln \text{ c} \\ e^(-1.76)=e^{\ln \text{ c}} \\ 0.1716=c \end{gathered}`

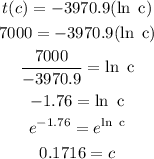
Therefore, A fossil that is 7,000 years old will have approximately of its carbon-14 remaining.​