Question

un club de 10 miembros tiene que elegir 3 officer's un presidente y un vicepresidente y un secretario de tesorería. si cada puesto es puesto puede tener solo una persona y no más de una persona puede tener más de un puesto, en cuentas maneras pueden esos puestos ser llenados ?

Answer 1

we can fill the available spots of 120 different ways

Step-by-step explanation:

This is a combinatorics problem. We need to choose 3 people of 10

The formula for combinatorics is:

`^nC^k=(n!)/(k!(n-k)!)`

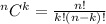
Where n is the total to choose from and k is the amount we're choosing.

Then:

`^(10)C^3=(10!)/(3!(10-3)!)`

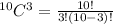
And now solve:

`^(10)C^3=(2\cdot3\cdot4\cdot5\cdot6\cdot7\cdot8\cdot9\cdot10)/(2\cdot3\cdot7!)`

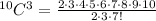
We can cancel out 2 and 3, and we can develop the 7!:

`^(10)C^3=(4\cdot5\cdot6\cdot7\cdot8\cdot9\cdot10)/(2\cdot3\cdot4\cdot5\cdot6\cdot7)`

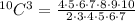
Now we can cancel out 4, 5, 6, 7

`^(10)C^3=(8\cdot9\cdot10)/(2\cdot3)=(8)/(2)(9)/(3)10=4\cdot3\cdot10=12\cdot10=120`

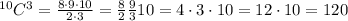
Thus, the answer is: we can fill the available spots of 120 different ways