To answer this question, we need to remember that the midpoint formula is given by:
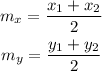
That is, we can find both coordinates for the midpoint of the segment EF applying it.
We know that the coordinates of E, and F are:
• E(2, 4)
,
• F(6, 8)
Then we can identify them as follows:
• E(2, 4) ---> x1 = 2, y1 = 4
,
• F(6, 8) ---> x2 = 6, y2 = 8
Therefore, we have that the midpoint of the segment EF is:
The x-coordinate is:

And the y-coordinate is:
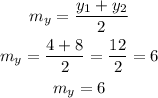
In summary, therefore, the midpoint of the segment EF is (4, 6).
We can check this if we see the following graph (showing only the extreme points and the midpoint):