SOLUTION
To answer the question, let us make a graph of the equation

The graph is shown below
(A) From the graph, the domain is determined from the x-axis. The domain is from -2 to +2,
Hence, the domain is
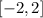
(B) The range is determined from the y-axis. The range from the graph is -1 to 1
Hence the range is
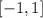
(C) We have the graph above already
(D) It is not a function because some values on the x-axis has two values on the y-axis. for example, where
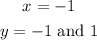
A function should have only one y value for each values of x.
Hence, it is not a function
(E) Since it is not a function, it is therefore not a one-to-one function
Hence, it is not a one-to-one function.