To answer this question, we need to check the kind of sequence we have here.
To check that, we need to subtract the second and the first term, the third and the second, and so on to check if the sequence is an arithmetic sequence. To check if it is a geometric sequence, we need to divide the second term by the first, the third by the second, and so on.
If we get a common number, it is called common difference in an arithmetic sequence, and common ratio in the geometric sequence.
We can check that the sequence is geometric since:
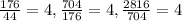
We have that the common ratio is equal to 4.
Then, the explicit formula for a geometric sequence is given by:
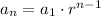
Then, we have that
a1 = 44
r = 4
The next four terms are:
n = 5, n = 6, n = 7, n = 8
The first of the next four terms (n =5):
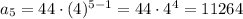
n = 6
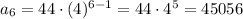
n = 7
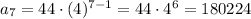
n = 8
![undefined]()