Question

Sketch the graph of the given functionh(x)= - 0.3(x- 10)^2 - 6

Answer 1

we have the equation

`h(x)=-0.3(x-10)^2-6`

this is a vertical parabola open downward (because the leading coefficient is negative)

Part 1

the vertex represents a maximum

the vertex is the point (10,-6)

Part 2

Vertical intercept

For x=0

h(x)=-0.3(0-10)^2-6

h(x)=-36

the vertical intercept is (0,-36)

Part 3

Horizontal intercepts

For h(x)=0

`\begin{gathered} 0=-0.3(x-10)^2-6 \\ -0.3(x-10)^2=6 \\ (x-10)^2=-20 \end{gathered}`

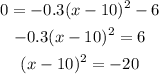
the graph has no real horizontal intercepts (complex numbers)

horizontal intercepts --------> DNE

see the attached figure to better understand the problem