Question

Question is down below For each point, determine if it’s is on the circle. If not, decide weather it is inside the circle or outside the circle, i. (4,0) ii. (-3,3)iii. (-2,-2) Fill in the blanks answer choices A. Inside B.outside C. on i. (4,0) will be located ____ the circle ii. (-3,-3) will be located ___ the circle iii. (-2,-2) will be loaded _____ the circle

Answer 1

We have to graph the circle with equation:

`(x-2)^2+(y-1)^2=25`

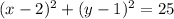
From the equation we can conclude that the center of the circle is at (x,y) = (2,1).

It also has a radius of √25 = 5 units.

We then can graph the circle as:

We have now to test if this points are on, inside or outside of the circle.

One way to do it is to calculate the distance to the center (2,1).

If the point is at a distance that is less than 5, the point is inside the circle.

If the point is at a distance that is more than 5, the point is ouotside the circle.

If the point is at a distance of exactly 5 units, the point is on the circle (NOTE: that can be the definition of the circle: all the points (x,y) that are at a distance r of a center (a,b)).

We can then calculate the distance for (4,0):

`\begin{gathered} d=\sqrt[]{(y_{}-y_c)^2+(x_{}-x_c)^2} \\ d=\sqrt[]{(y-1)^2+(x-2)^2} \\ d=\sqrt[]{(0-1)^2+(4-2)^2} \\ d=\sqrt[]{(-1)^2+(2)^2} \\ d=\sqrt[]{1+4} \\ d=\sqrt[]{5}<5\longrightarrow\text{Inside} \end{gathered}`

We can calculate the distance for (-3,-3) as:

`\begin{gathered} d=\sqrt[]{(y-1)^2+(x-2)^2} \\ d=\sqrt[]{(-3-1)^2+(-3-2)^2} \\ d=\sqrt[]{(-4)^2+(-5)^2} \\ d=\sqrt[]{16+25} \\ d=\sqrt[]{41}>5\longrightarrow\text{Outside} \end{gathered}`

We can calculate the distance for (-2,-2) as:

`\begin{gathered} d=\sqrt[]{(y-1)^2+(x-2)^2} \\ d=\sqrt[]{(-2-1)^2+(-2-2)^2} \\ d=\sqrt[]{(-3)^2+(-4)^2} \\ d=\sqrt[]{9+16} \\ d=\sqrt[]{25} \\ d=5\longrightarrow\text{ On the circle} \end{gathered}`

We can check in the graph as:

Answer:

i. (4,0) will be located inside the circle

ii. (-3,-3) will be located outside the circle

iii. (-2,-2) will be loaded on the circle