Question

Kevin buys a truck for $52,000 and it decreases in value 12.5% every year, How many years will it take for the truck to be worth $30,000 (Use log method, nearest whole number)

Answer 1

Given :

Principal P= $52000

Interest rate r=12.5 %

Let x be the number of yers

The worth p(x) is $30000 after x years.

The math model for worth is

`P(x)=P(1-(r)/(100))^x`

Substitute P(x)=30000, P=52000, r=12.5, we get

`30000=52000(1-(12.5)/(100))^x`

`30000=52000((100)/(100)-(12.5)/(100))^x`

`30000=52000((100-12.5)/(100))^x`

`30000=52000((87.5)/(100))^x`

`30000=52000(0.875)^x`

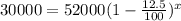
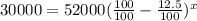
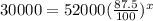
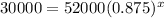
Dividing both sides by 52000, we get

`(30000)/(52000)=(52000)/(52000)(0.875)^x`

`0.577=0.875^x`

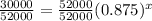
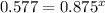
We know that

`b^x=y\text{ then }log_by=x`

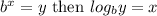
Here b=0.875 and y=0.577.

`\log _(0.875)0.577=y`

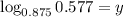
Using the change base formula.

`\log _ax=(\log _bx)/(\log _ba)`

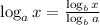
Take b=10, and substitute a=0.875 and x=0.577, we get

`\log _(0.875)0.577=(\log _(10)0.577)/(\log _(10)0.875)`

`\text{ Use }\log _(10)0.577=-0.238\text{ and }\log 0.875=-0.058.`

`\log _(0.875)0.577=(-0.238)/(-0.058)=4.103`

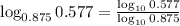
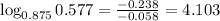
Taking the nearest whole number.

`\log _(0.875)0.577=4`

Hence the number of years =4.