Given:
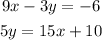
To determine the solutions of the given system of equations, we first solve for x in 9x-3y=-6:
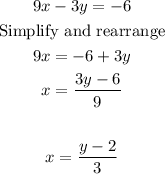
Next, we substitute x =(y-2)/3 into 5y=15x+10. So,
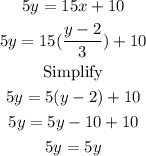
Since 5y=5y is redundant information, this is a dependent system. Therefore, the given system of equations have infinitely many solutions.