Question

hi there ms or mr could you please help me out with this problem? oh yeah no this isn't a test my teacher put this up as practice work but still could you help me out please?

Answer 1

The angles BCD and ACB are suplementary, because they form an angle of 180 degrees when joined together. We know the value of BCD so we can calculate the value of ACB. We have:

`\begin{gathered} \measuredangle BCD+\measuredangle ACB=180 \\ 6x+2+\measuredangle ACB=180 \\ \measuredangle ACB=180-6x-2 \end{gathered}`

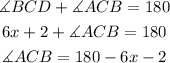
The sum of the internal angles on a triangle is equal to 180 degrees. The three internal angles on this triangle are: BAC, ACB and ABC. We can calculate the value of "x" by adding all of them and making it equal to 180.

`\begin{gathered} \measuredangle BAC+\measuredangle ACB+\measuredangle ABC=180 \\ 3x+15+180-6x-2+2x-1=180 \\ 3x-6x+2x+15+180-2-1=180 \\ -x+192=180 \\ -x=180-192 \\ -x=-12 \\ x=12 \end{gathered}`

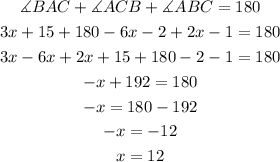
The value of "x" is 12.