Question

Use the description of the pair of lines given below to find the slopes of Line 1 and Line 2.

Answer 1

The slope formula is:

`m=(y_2-y_1)/(x_2-x_1)`

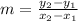
First, let's solve the slope for Line 1.

a. Subtract y₁ from y₂.

`-10-5=-15`

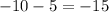
b. Subtract x₁ from x₂.

`3-0=3`

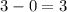
c. Divide the result in step a by the result in step b.

`-15/3=-5`

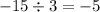
Hence, the slope of Line 1 is -5.

Let's now solve the slope of Line 2. Use the same steps above.

a. Subtract y₁ from y₂.

`38-3=35`

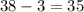
b. Subtract x₁ from x₂.

`6-(-1)=7`

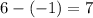
c. Divide the result in step a by the result in step b.

`35/7=5`

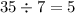
Hence, the slope of Line 2 is 5.