Question

Please Help I'm Stuck with this

Answer 1

a)4cm b)5cm

Explanation:

a)

`Solution,\\\\Length(l)=8cm\\\\Breadth(b)=2cm\\\\Now,\\\\Area=l*b\\\\Area=8cm*2cm\\\\Area=16cm^(2)`

Area of the rectangle is 16cm².

When,

Area of the rectangle is equal to the area of the square then,

Area of square=16cm²

Now,

→Length=√Area

→Length=√16cm²

→Length=4cm

b)

`Solution,\\\\Length(l)=8cm\\\\Breadth(b)=2cm\\\\Now,\\\\Perimeter=2(l+b)\\\\Perimeter=2(8cm+2cm)\\\\Perimeter=2(10cm)\\\\Perimeter=20cm`

The perimeter of rectangle=20cm

When,

The perimeter of the rectangle is equal to the perimeter of the square then,

The perimeter of square=20cm

Now,

Length=Perimeter/4

Length=20cm/4

Length=5cm

Answer 2

a) 4 cm

b) 5 cm

Explanation:

a) Area of a rectangle = width x length

From inspection, the width of this rectangle is 2 cm and the length is 8 cm

⇒ area of the rectangle = 2 x 8 = 16 cm²

A square has 4 sides of equal measure.

Let the side of a square =
`x`

Therefore, the area of a square =
`x * x = x^2`

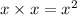
If the square has the same area as the rectangle, then

`x^2=16`

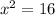
Square root both sides:
`x = √(16) =\pm4`

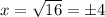
Since the length of a side cannot be negative,
`x=4` only

So the side length of the square = 4 cm

b) Perimeter of a rectangle = 2 x length + 2 x width

⇒ perimeter of the rectangle = (2 x 8) + (2 x 2) = 20 cm

Since the side lengths of a square are equal, and a side length =
`x`

Perimeter of a square = 4 x
`x` = 4
`x`

If a square has the same perimeter as the rectangle, then

`4x=20`

Divide both sides by 4:
`x=20 / 4 = 5`

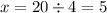
side length of this square = 5 cm