Question

Is the information in the diagram enough to show WXYZ is a parallelogram? Explain. please help me.

Answer 1

We know that the four angles of a quadrilateral must sum up to 360º. So, we have:

`X+Z+W+Y=360^(\circ)`

Since X and Z are congruent, and W and Y are congruent, we have:

`\begin{gathered} X+X+W+W=360^(\circ) \\ \\ 2X+2W=360^(\circ) \\ \\ 2(X+W)=360^(\circ) \\ \\ X+W=180^(\circ) \end{gathered}`

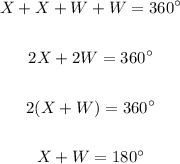
Thus, X and W are co-interior angles, which means segments XY and XZ are parallel.

And since Y and W are congruent, X and Y are also co-interior angles, which means segments XW and YZ are parallel.

Therefore, WXYZ is a parallelogram.