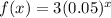Exponential decay is when an original amount is reduced by a consistent rate over a period of time, is generally expressed in percent change.
Exponential functions are represented by:

Then, a percent rate of decrease of 5% is equal to 0.05 in decimal form.
Therefore, the function that has this decay factor is: