Question

Suppose that you are offered the following "deal." You roll a six sided die. If you roll a 6, you win$13. If you roll a 4 or 5, you win $4. Otherwise, you pay $6.a. Complete the Table: List the X values, where X is the profit, from smallest to largest. Round to4 decimal places where appropriate.Probability Distribution TableХP(X)b. Find the expected profit. $(Round to the nearest cent)

Answer 1

We have a six-sided die

possible outcome

`1,\text{ 2,3,4,5,6}`

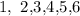
if you roll a 6 you get $13

if you roll a 4 or 5 you get $4

if otherwise, you get 1,2,3 you will them $6

`\begin{gathered} \text{Probability of getting \$13=}(1)/(6) \\ \\ \text{Probability of getting \$4=}(2)/(6)=(1)/(3) \\ \\ \text{Probability of paying them \$6=}(3)/(6)=(1)/(2) \end{gathered}`

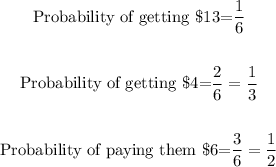
We are asked to complete the table from smallest to biggest

Part B

The expected profit.

`\begin{gathered} -6((1)/(2))+4((1)/(3))+13((1)/(6)) \\ \\ =-3+(4)/(3)+(13)/(6) \\ =\text{ \$0.50} \end{gathered}`

Part C

If you play many games you will likely win on average very close to $0.50 per game because the expected profit is $0.50

Part D

Yes, since the expected value is positive you will likely to come home with more money if you played more games