Question

State whether the relationship between the variables in the table is a direct variation, an inverse variation, or neither. If it is a direct or inverse variation, write a function to model it.

Answer 1

Given: A table of values of x ad y

To Determine: The type of relationship that exist between x and y

Solution

Differentiate between a direct and an inverse variation

Direct variation occurs when an increase in one variable is results with an increase in value of the other variable. Inverse variation occurs when an increase in one variable is results with a decrease in value of the other variable

From the table given, it can be observed hat as x increases, y also increases. Therfefore, the relationship that exists between x and y is direct variation

Determine the function to model the relationship between x and y

`\begin{gathered} Rate\text{ of change of y to the rate of change of x} \\ (y_2-y1)/(x_2-x_1)=(y_3-y_2)/(x_3-x_2)_ \\ (27-9)/(9-3)=(39-27)/(13-9) \\ (18)/(6)=(12)/(4) \\ 3=3 \end{gathered}`

Since the rate of change of to rate of x, hence, the relation is a linearrelationship

Using the general equation of a straight line to get the equation using two given points

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ Using\text{ two points below} \\ Point1:(3,9) \\ Point2:(9,27) \end{gathered}`
`\begin{gathered} So, \\ (y-9)/(x-3)=(27-9)/(9-3) \\ (y-9)/(x-3)=(18)/(6) \\ (y-9)/(x-3)=3 \\ y-9=3(x-3) \\ y-9=3x-9 \\ y=3x-9+9 \\ y=3x \end{gathered}`

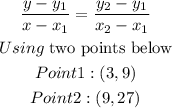
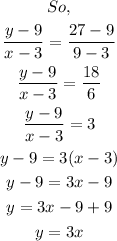
In Summary,

The relationship between x and y is DIRECT VARIATION

The function that model the relationship between x and y is y = 3x