Question

The population of a town increased by 10%, and 20%across two successive years. What is the net increasein the population, across the two years?

Answer 1

32%

Explanation:

Let the initial population of the town = x

First Year

In the first year, the population increases by 10%.

`\begin{gathered} \text{Population after first year}=x+(10\%\text{ of x)} \\ =x+0.1x \\ =1.1x \end{gathered}`

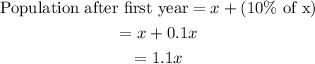
Second Year

In the second year, the population increases by 20%.

`\begin{gathered} \text{Population after second year}=1.1x+(20\%\text{ of 1.1x)} \\ =1.1x+(0.2*1.1x) \\ =1.1x+0.22x \\ =1.32x \\ =(1+0.32)x \\ =(1+(32)/(100))x \end{gathered}`

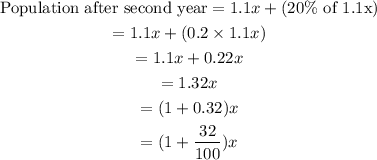
We see at the end of the second year, the initial population, x has increased by 32%.

The net increase in the population across the two years is 32%.