SOLUTION
This is a geometric series question and we knkow this because we were given a common ratio (r) value.
The formula for calculating the sum of a GP, where r>1 is:
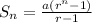
Where a=4, r=4, and n=7
Now, Substituting these given parameters into the formula above, we will have:

Final answer.
The sum of the first seven terms of this geometric series is 21844.