Both linear functions will intersect at the same point, meaning, the x y coordinates are the same. So you have to equate both equations and clear the value of x:

Now using either function you have to calculate the value of the corresponding y-coordinate, for explanation purposes I'll do it with both:
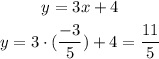
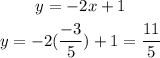
As you see, using either function to calculate the y-coordinate is the same.
The functions intersect in point (-3/5, 11/5)