Question

Find the missing one. Round the radius and central angle to the nearest whole number. Round the arc length to two decimal places. (use 3.14 as pi)

Answer 1

Given:

radius = 6ft

area of a sector = 59.66 ft²

π = 3.14

Find: central angle (missing one)

Solution:

To solve for the central angle given radius and area of a sector, we have the formula below:

`AreaofaSector=(\theta)/(360)(\pi r^2)`

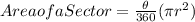
Let's plug in the given data above to the formula.

`59.66ft^2=(\theta)/(360)(3.14)(6ft)^2`

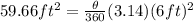
Then, solve for θ.

`\begin{gathered} 59.66ft^2=(113.04ft^2\theta)/(360) \\ 59.66ft^2=0.314ft^2\theta \\ \text{Divide both sides by 0.314ft}^2 \\ (59.66ft^2)/(0.314ft^2)=(0.314ft^2\theta)/(0.314ft^2) \\ 190=\theta \end{gathered}`

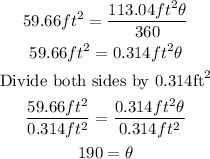
Therefore, the measure of the central angle is 190 degrees.

To summarize:

radius = 6ft

central angle = 190 degrees

area of a sector = 59.66 ft²