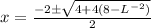To solve x;
1. Mulriply both sides of the equation by the denominator of the fraction in the right:
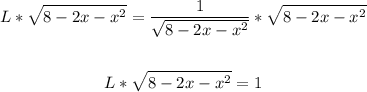
2. Divide both sides of the equation into L:
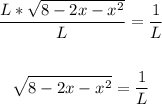
3. Square both sides of the equation:
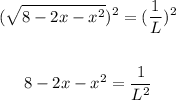
4. Rewrite the term in the right with a negative exponent:

3. Rewrite the equation in the form ax^2+bx+c=0
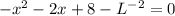
Use the quadratic formula to solve x:

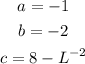
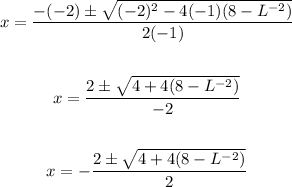
Answer: