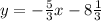Answer:
Step-by-step explanation:
A line equidistant from the points (-11, -8) and (-1, -2) will be a line perpendicular to the given line.
Step 1: Find the midpoint of the line
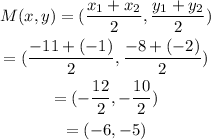
Step 2: Find the slope of the line:
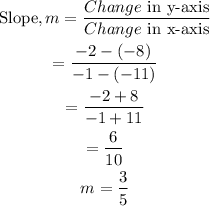
• Two lines are perpendicular if the product of their slopes is -1.
Since the new line is perpendicular, its slope will be:
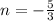
Step 3: Find the equation of the line
We are then to find the equation of a line passing through (-6,-5) with a slope of -5/3.
Using the point-slope form:

We have:
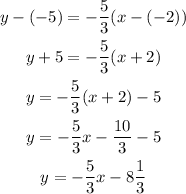
The equation of the line equidistant from the points (given in slope-intercept form) is: