Solution:
Let the car efficiency of first car be x
Let the car efficiency of the second car be y
Given that the first car consumed 20 gallons of gas and the second consumed 40 gallons of gas. The two cars drove a combined total of 1200 miles
This can be represented as
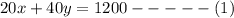
Given that the sum of their fuel efficiencies was 45 miles per gallon
This can be represented as

Solve both equations simultaneously
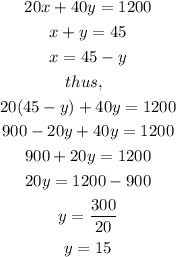
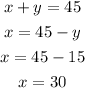
Thus,
First car: 30 miles per gallon
Second car: 15 miles per gallon